Tunneleffekt
"In der Quantenwelt ist es möglich, sich durch eine energetisch verbotene Zone schnell hindurchzumogeln."
(Richard Feynman)
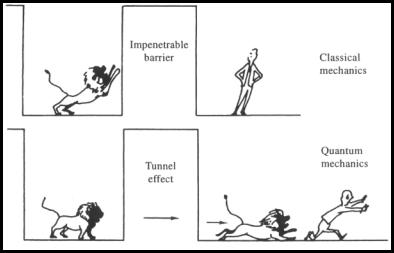 | In der klassischen Physik kann ein Teilchen eine Barriere nicht überwinden, deren potentielle Energie höher ist als die kinetische Energie des Teilchens. In der Quantenmechanik wird einem Teilchen eine Welleneigenschaft mit Wellenfunktion Ψ zugeordnet. Das Betragsquadrat |Ψ|² wird als Wahrscheinlichkeitsdichte für den Ort des Teilchens interpretiert. Die Wellenfunktion nimmt mit zunehmender Eindringtiefe in die Barriere exponentiell ab, ist aber weder innerhalb der Barriere noch dahinter Null. |
sdf \[ a_1^2 + a_2^2 \] as d
Tunneleffekt
"In der Quantenwelt ist es möglich, sich durch eine energetisch verbotene Zone schnell hindurchzumogeln."
(Richard Feynman)
Die Schrödingergleichung
| Gebiet I |
| Gebiet II |
| Gebiet III |
|---|---|---|---|---|
| \[ \begin{aligned} -\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \Psi = E\cdot \Psi \end{aligned} \] | \[ \begin{aligned}-\left(\frac{\hbar^2}{2m} \frac{d^2}{dx^2} +V_0 \right) \Psi = E\cdot \Psi\end{aligned} \] | \[ \begin{aligned} -\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \Psi = E\cdot \Psi \end{aligned} \] | ||
| bzw. | ||||
| \[ \begin{aligned} \frac{d^2}{dx^2} \Psi = -\frac{2mE}{\hbar^2}\cdot \Psi \end{aligned} \] | \[ \begin{aligned} \frac{d^2}{dx^2} \Psi = -\frac{2m(E-V_0)}{\hbar^2}\cdot \Psi \end{aligned} \] | \[ \begin{aligned} \frac{d^2}{dx^2} \Psi = -\frac{2mE}{\hbar^2}\cdot \Psi \end{aligned} \] |
Jede der Gleichungen hat je zwei unabhängige Lösungen. Um eine Lösung für das gesamte Gebiet zu bekommen müssen die drei einzelnen Lösungen so zusammengesetzt werden, dass die Übergänge stetig und stetig differenzierbar sind. Eine mögliche solche Lösung lautet